
Így tanítunk mi - játékos ismerkedés az algoritmusokkal
Ez a bemutató a “Programozó logika ovisoknak – 90 napos kihívás” programunkhoz készült azzal a céllal, hogy megmutassuk, miként segítünk egy óvodás korú gyereknek játékosan ismerkedni az algoritmusokkal, és elsajátítani a kódolás logikai alapjait.
Kutatások igazolják, hogy azoknak a gyerkőcöknek, akik már egészen kicsi korukban megtanulnak kódolni, később fejlettebbek lesznek a logikai képességeik, jobban rááll az agyuk az ok-okozati összefüggésekre. Emellett kitartóbbak, magabiztosabbak, kreatívabbak és jobb problémamegoldók is, mint a társaik. Sokszorosan megtapasztalják, hogyha szisztematikusan nekiállnak egy kihívás megoldásának, lépésről lépésre haladnak miközben folyamatosan ellenőrzik magukat, akkor az erőfeszítéseiket siker fogja koronázni.
Ezért tartottuk nagyon fontosnak, hogy ilyen “képzés” legyen magyar nyelven is, hiszen ezeket a logikai alapokat egy nyugati vagy skandináv oktatásban cseperedő gyerek ma már természetes, hogy megkap.
Kezdjünk bele!
Az 5 éves Tomi történetét fogjuk itt most hosszasan mesélni, aki részt vett a programunk tesztelésében. Egy-egy gyakorlatot emelünk ki minden logika kapcsán, de a foglalkozástervekben 15-20 ötletet hozunk, milyen tevékenységekkel, játékokkal lehet elmélyíteni az adott logikát a gyerek fejében, plusz ott vannak még a feladatlapok is.
Na de most már tényleg kezdjünk bele!
A program elején az alábbi táblát helyeztük Tomi elé. Igen, ez a tábla 4 db tojástartóból lett összerakva. A program során mi magunk is meglepődtünk, hogy hányféle otthon található dologból lehet pályát készíteni. A lényeg, hogy a tojástartón belül minden tojásnak szánt mélyedés egy mező.

Ahogy látjátok, vannak mezők, amelyek cukorkát rejtenek (Tomi anyukájának a duginasis rejtekhelyéről vettük kölcsön), vannak mezők, amiket láva borít (piros labdák), ezeket értelemszerűen el kell kerülni.
Tomi azt a feladatot kapta, hogy a LEGO kalózt irányítsa, és a lávás mezőket elkerülve szedje össze a cukorkákat. Extra motivációt jelentett, hogy a cukrokat el is fogyaszthatta, ha a kalózzal megszerezte. A kalóz irányításához az alábbi karakterkészletet használhatta.
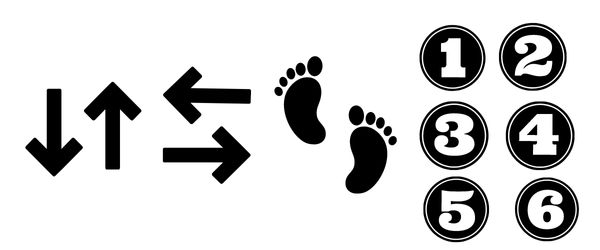
A nyilakkal állíthatta be, hogy merre forduljon a kalóz, a lépés jel azt jelentette, hogy előre lép, a számokkal pedig azt tudta megadni, hogy hányat lépjen egyszerre.
Na hát első próbálkozásra egy fél óra alatt sikerült kirakni az alábbi algoritmust. Persze Tomi nem tudta, hogy algoritmust kell “írnia”, ezt a kifejezést egyszer sem hallotta a program során.
Ha azt gondoljátok, könnyen ment, akkor tévedtek. A fél óra alatt rengeteg felnőtt segítségre volt szükség, és Tomi egy ponton inkább valami mást akart játszani, mert az első pár próbálkozás során nem szerzett túl sok sikerélményt. Ráadásul ugye ez a kódsor még csak egyetlen cukorka begyűjtését eredményezte a kalóz számára. Az abban a pillanatban teljesen lehetetlennek tűnt, hogy Tomi kirakjon egy ennél nyolcszor hosszabb kódot, és végigvezesse a cukorkás mezőkön a kalózt.
DE mi ennek nagyon örültünk, mert az volt a hipotézisünk, hogy egy 5 éves gyereknek ez a feladat elsőre még túl nehéz lesz. Ezt a feladatot a program kétharmadánál terveztük bevetni, és Tomi igazolta, hogy szükség van az alapozó játékokra, foglalkozásokra ahhoz, hogy ilyen bonyolultságú algoritmusokat tudjon írni egy óvodás gyerkőc.
Úgyhogy belekezdtünk az alapozásba…
Alapozás
A tematikánk szerint csak a 8. héten kezdünk el konkrétan az algoritmusokkal foglalkozni. Előtte megalapozzuk az algoritmusokkal kapcsolatos logikai gondolkodást. Nézzük lépésenként, hétről-hétre, hogy miket tanultunk Tomival!
Sorrendiség
Az algoritmusokon belül a műveleteknek általában megszabott sorrendjük van, így fontos logikai alapnak számít, hogy a gyerek fejében is egyértelmű legyen ez. Ezért az első héten a sorrendiséget gyakoroljuk számtalan játékkal és foglalkozással.
Ezek közül az egyik, hogy jól ismert történetek részleteit keverjük össze, és rendezzük sorba. Tomi testvére egy sulis előadáson tavaly szerepelt a Békakirály című darabban, úgyhogy ez volt az egyik történet, amit részekre bontottunk. Készítettünk hozzá illusztrációkat is, de más történeteknek a részleteit Tomival rajzoltattuk meg, és volt olyan is, amit csak a szavak szintjén beszéltünk át.

A feladat itt az volt, hogy rendezzük sorba a jeleneteket a történeten belül. Ha valaki nem ismerné, nem arról van szó, hogy a királylánynak nem tetszett a herceg, és addig csókolgatta, amíg békává nem változott 😉
Szintézis
Ez azt a folyamatot takarja, amikor egy műveletet részműveletekre bontunk. Kétféle ember van: akiket megrémiszt egy középiskolai matek egyenlet és akiket nem. Akiket megrémiszt, ők egyben látják az egyenletet. Egy feladatot látnak: az egyenlet megoldását. Akiket nem rémiszt meg, ők több részfeladatot látnak. Azt látják, hogy a megoldáshoz el kell végezni egy egyszerű osztást, aztán egy egyszerű kivonást, aztán egy egyszerű szorzást, aztán megint egy osztást, majd végül egy összeadást.
Mivel összeadni, szorozni, osztani mindenki tud, így nyilván őket nem rémiszt meg egy egyenlet. Ha a részfeladatokat látná mindenki, valószínűleg jóval kevesebben rezelnének be egyenletekről. De az helyzet sajnos az, hogy nem vagyunk elég ügyesen a feladatok részfeladatokra történő lebontásában.
A célja ennek a hétnek az volt, hogy Tomi viszont az legyen, hiszen a jó problémamegoldó emberek igazából ebben az egy dologban jobbak a többieknél. Ügyesebben bontják részekre a feladatokat.
Márpedig Tominak ehhez szüksége volt ahhoz, hogy majd a kalóz irányításakor ne egyszerre akarja az összes cukrot felvenni (az túl nehéz feladat), hanem először csak a legközelebbit nézze ki, majd az ahhoz legközelebbit, és így tovább.
Ehhez is cselekményeket használtunk, de ezúttal békák és hercegek helyett hétköznapi tevékenységekről beszélgettünk (és csináltuk is őket). Porszívózás, fogmosás, mosogatás. Olyan tevékenységek, amiket már Tomi is jól ismert, de ennyire részleteiben még talán nem gondolkodott róluk.
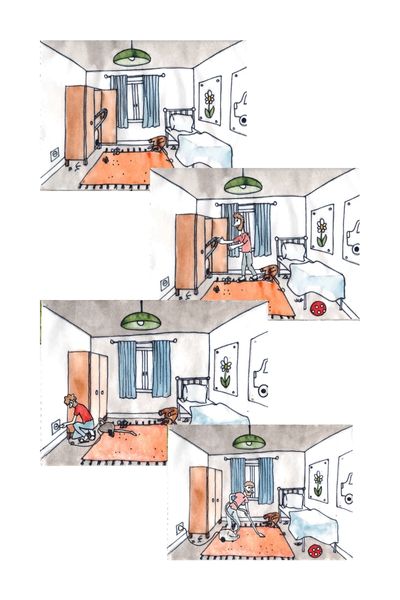
Ezekhez a hétköznapi tevékenységekhez is készítettünk illusztrációkat, úgyhogy itt is össze tudtuk keverni a sorrendet, hogy aztán Tomi sorba rakja őket.
Az első két feladatlaphoz annyi illusztrációt készítettünk egyébként, hogy kiadhatnánk belőlük egy mesekönyvet. Ezeket egyébként kézzel rajzoltuk, és úgy digitalizáltuk utólag.

Feltételek ellenőrzése
Az életben és az informatikában is a legtöbb algoritmusban vannak olyan műveletek, amik feltételhez vannak kötve. Ha esik, esernyőt viszünk. Ha hideg van, kabátot veszünk. Ha szombat van, délig alszunk (már aki).
A számítástechnikában pl. a Facebookon csak akkor láthatod, mit posztolok, HA az ismerősöm vagy. A tojástáblán csak akkor léphetsz az adott mezőre, ha nem borítja LÁVA. Tominak tehát ezt a logikai alapot is el kellett sajátítania, hogy sikereket érhessen el a kalózzal.
Talán ehhez a “leckéhez” találtuk ki a legtöbb játékot és feladatot. Gyakorlatilag végtelen lehetőségünk van. Minden szortírozós feladat, minden ha…, akkor… típusú kihívás jó ennek a gyakorlására.
A kedvencünk az volt, amikor a Tomi fejére harisnyát húztunk, benne egy teniszlabdával. Felállítottunk fél literes kis flakikat és nagy kólás flakikat. A feladata az volt, hogy a kólás flakikat feldöntse egyfajta buldózerként, de a kis flakikat hagyja állva.
Feltételek ellenőrzése újra
Még egy extra hetet szántunk a feltétel ellenőrzés témájának, mert hihetetlenül fontosnak tartottuk/tartjuk. Ezen a második héten már egy kicsit bonyolítottunk a dolgon, ugyanis nem A és B esetek voltak, hanem több lehetséges feltétellel dolgoztunk.
Lehet A és B és C feltétel is. Lehet A, B, C, D, E, F, G és H feltétel is. Lehet olyan sok feltétel, hogy nem is ismerjük az összes lehetségest. Jó példa erre a szolnoki vasútállomás, ahol fogalmam sincs, hogy milyen vonatok állnak meg. Azt az egyet tudom, hogy a Szegedi IC-re fel kell szállnom, míg az összes többi vonat érkezése esetén ott kell maradnom a peronon.
Sok színezős, karikázós gyakorlatot használtunk. Talán a legegyszerűbb az volt, amikor 3 különböző alakzatot 3 különböző színűre kellett kiszínezni.

Blokkosítás
Vannak olyan műveletsorok, amiket már annyira jól ismerünk, olyan rutinszerűen végzünk el, hogy egy saját nevet kap. Az informatikában akkor beszélünk ilyesmiről, amikor a programozó ír egy függvényt, aminek a nevét használva később hivatkozik rá. Nem kell mindig újraírnia a műveleteket a függvényen belül, hanem csak beírja a függvény nevét, és a számítógép már tudja is, hogy minek kell történnie.
A hétköznapi életben ilyen az óvodába jutás. Nem soroljuk végig, hogy beülünk a kocsiba, balra kanyarodunk, elmegyünk a főútig, ott jobbra kanyarodunk, elmegyünk a Petőfi Sándor utcáig, ott lefordulunk, stb. Ehelyett csak annyit mondunk, hogy megyünk az oviba.
Hétköznapi tevékenységek során tudtuk ezt Tominak is leginkább megtanítani. Például megtanultunk panírozni. A panírozás elsőre még egy komoly műveletsor volt 3 tényárral, egyikben liszt, egyikben tojás, egyikben kenyérmorzsa. Plusz egy negyedik tányérba gyűjtöttük a kész, süthető húsokat.
De amikor ez már jól ment, következő héten a recept már ezt a rengeteg műveleti elemet nem tartalmazta, csak panírozásként hivatkozott rá. Tomi pedig tudta, hogy mi a feladat.
Loopok
Loopokról akkor beszélünk, amikor egy műveletet vagy egy műveleti blokkot megismétlünk. Lehet olyan eset is, amikor egy konkrét darabszámunk is van, hogy hány ismétlésre van szükség. Ilyeneket kell Tominak megadnia a kalóz számára, amikor azt akarja, hogy pl. hármat lépjen előre.
De létezik olyan eset is, amikor valamilyen feltétel teljesüléséig kell ismételgetnünk a műveletet. Pl. addig panírozni a húsokat, amíg el nem fogy a kikloffolt hús. Vagy addig menni előre, amíg falnak nem ütközünk.
Ehhez nagyon jó szinezős feladatokat találtunk ki 🙂
Dubugging
Ez a hibakeresést jelenti az informatikában. De igazából bármilyen probléma megoldása közben előny, ha szisztematikusan tudjuk ellenőrizni magunkat és a munkánkat. Tominak is szüksége volt erre, mert sokkal könnyebben irányította a kalózt, amikor elkezdte a saját maga által lerakott kódokat ellenőrizni. Észrevette, ha nem pont a cukorkára lép vagy ha neadjisten lávára lép a kalóz.
Ennek a gyakorlásához nyilván egy csomó kakukktojás kereső karikázgatós klasszzikus feladatot is vittünk Tomiéknak, de talán a legemlékezetesebb az volt, amikor Tomi szülei öltözékében kellett a hibát keresni. Tomi apukája felvett valamit, ami Tomi anyukájához tartozott, és fordítva ugyanez, a gyereknek pedig meg kellett keresnie az öltözéken a bugot.
Ez nagyon sok közös nevetést eredményezett, úgyhogy hatalmas sikerként éltük meg mi is 🙂
Algoritmusok követése
A program ezen pontján érkezünk el az algoritmusokig. Itt még nem Tomi írja őket, csak követjük az utasításokat. Először ember nyelven szóló utasításokat követünk, majd megismerkedünk karakterkészletekkel, amikor nyilak és egyéb képek, ikonok közvetítik az utasításokat.
Tomi a hét végén már gyönyörűen tudta olvasni ezeket a “parancsokat”. Tojástartó helyett ezúttal a kertben rajzoltuk fel a pályát krétával a betonra. Apa írta a karakterkészlettel az utasításokat, és Tominak kellett ezt lefordítania a “robot” anyukája számára. Anya volt tehát a robot, akit Tomi irányított. De a parancsokat még nem ő írta, csak segített a robotnak értelmezni azokat.
Újra kalózkodunk
Ezt követően vettük elő újra a tojástartót, a cukorkákat, a lávalepte mezőket és a kalózt. Tomi már jól ismerte a karakterkészletet, hiszen anyukáját több ízben is sikeresen irányította ezek alapján.
Nem okozott gondot a loopok használata sem, ügyesen bánt a lépések számosságával. Alműveletekre bontotta a feladatot, tehát mindig csak a legközelebbi cukorhoz próbálta navigálni a kalózt. Így sokkal emberibbnek, átláthatóbbnak, egyszerűbbnek tűnt a feladat.
A lávás mezőket elkerülve ügyesen összeszedte a cukorkákat 8 héttel az első sikertelen próbálkozás után.

Hogyan tovább?
Maradt még a kihívásból 3-4 hetünk, és számtalan ötletünk, hogy miként bonyolíthatjuk tovább a problémákat, amiket Tomi megoldhat. Számtalan lehetőség a karakterkészlet bővítésére, új típusú akadályok bevezetésére, stb.
Az utolsó hetek történéseit már tényleg csak azokkal oszthatjuk meg, akik csatlakoznak a kihíváshoz, de nagy vonalakban annyi történt, hogy egyre összetettebb, történet alapú kihívás elé állítottuk Tomit. Ő pedig egyre bonyolultabb algoritmusokat írt, és ügyesen megoldotta őket.
Reméljük, kedvet kaptál, hogy csatlakozz a 90 napos kihívásunkhoz. Ha igen, kattints a linkre. Minden további információt ott találsz 🙂
